EZRでPearson(ピアソン)の積率相関係数の計算と検定をする方法

EZRを使用すれば、Pearson(ピアソン)の積率相関係数を計算し、検定を簡単にすることができます。

それでは、EZRで計算と検定をする手順を例題を交えてわかりやすく説明すると共に結果の見方を解説していきましょう！！

使用するデータ
【重要！】ピアソンの積率相関係数を計算する条件
EZRでピアソンの積率相関係数を【計算し、検定する方法】
EZRの結果の見方
1. 補足(結果の意味を日本語に翻訳)
参照・参考文献・書籍
【まとめ】相関係数の解説

使用するデータ

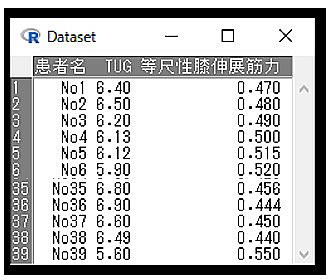
よくある話ですが、このように地域在住の高齢者のTUGと等尺性膝伸展筋力のデータを収集したとします。

データ

散布図

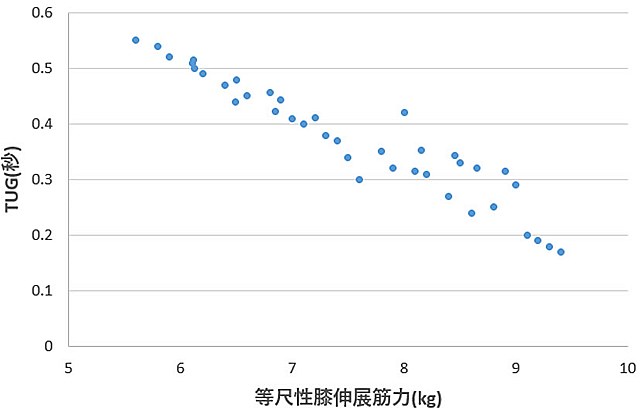
ここではこのデータを使って説明しようと思います。

目次に戻る

【重要！】ピアソンの積率相関係数を計算する条件

まず、ピアソンの積率相関係数を計算する前提条件として、

1.変数が連続変数である。
2.データが正規分布に従っている。
3.外れ値がない。

を満たす必要があります。

では、詳しく説明していきましょう。

目次に戻る

変数が連続変数である

ピアソンの積率相関係数を計算するには、変数が連続変数でなくてはいけません。

ここでは、TUGと等尺性膝伸展筋力の相関関係を求めるので、

変数は、TUG, 等尺性膝伸展筋力となります。

TUGや等尺性膝伸展筋力は量的なデータで、連続変数でありますから、
ピアソンの積率相関係数を計算することができます。

連続変数や尺度の話はこちらでしています。

【FIMやMMTは間隔尺度？順序尺度？】リハビリで使用する尺度は、何尺度か？

リハビリ統計でよく使う尺度の解説と【尺度の例(FIM, MMT, ROMなど)】を掲載しています。

目次に戻る

データが正規分布に従っている

ピアソンの積率相関係数を計算するには、変数のデータそれぞれが正規分布に従っている必要があります。

つまり、TUGや等尺性膝伸展筋力のデータが正規分布に従っている事を確認する必要があります(TUGのデータも正規分布、等尺性膝伸展筋力のデータも正規分布に従っている必要がある)。

EZRでは、正規分布に従っているかをを検定する方法として、Kolmogorov-Smirnov検定やSharpiro-Wilk検定を用いる事ができます。

＊ちなみに、今回使用したデータは正規分布に従っていません。本当はこのデータではピアソンの積率相関係数を計算することはできません(使い方の説明をする為なので気にしないでください。)

目次に戻る

外れ値がない

ピアソンの積率相関係数は、外れ値の影響を受けやすいので、外れ値の有無を検討する必要があります。

EZRでは、外れ値の検定としてSmirnov-Grubbs検定を使用することができます。

＊外れ値とは他とは大きくかけ離れた値の事。この赤印のような値の事です。

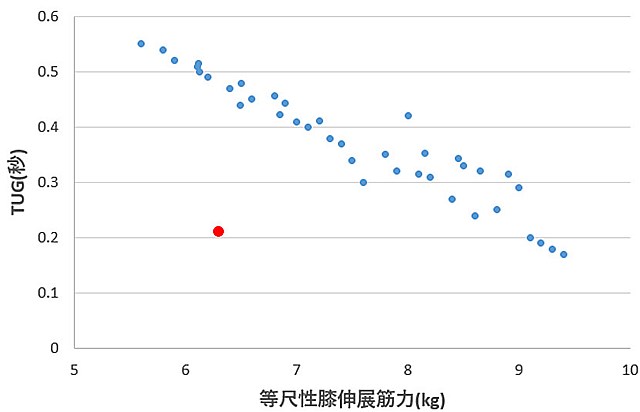
＊外れ値を除外すべきかはよく考える必要があります。

目次に戻る

EZRでピアソンの積率相関係数を【計算し、検定する方法】

では、上記の条件を満たしている事を確認したら、さっそくEZRでピアソンの積率相関係数を計算し、検定していきましょう！

1.EZRを起動して、データを読み込みます。

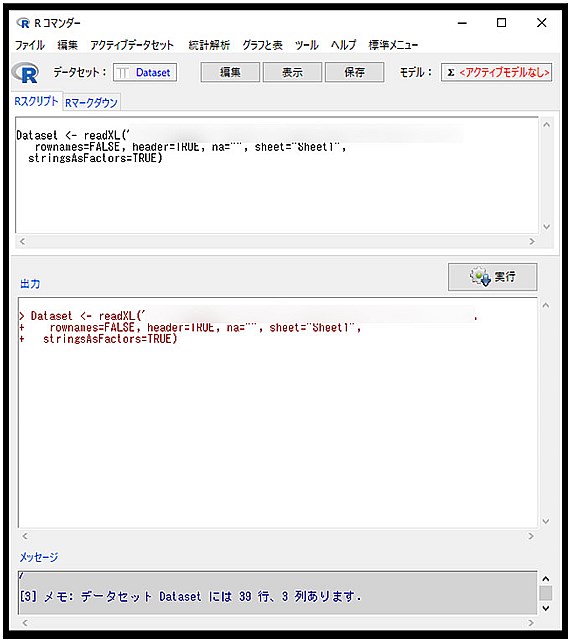
2.次に統計解析を選択します。

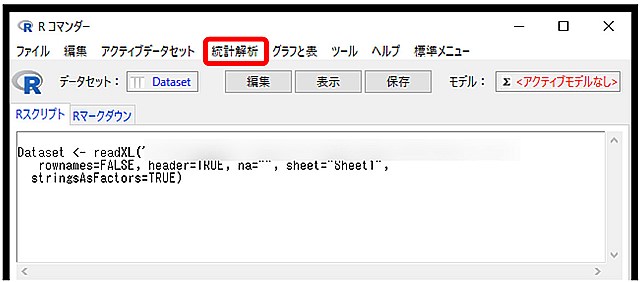
3.連続変数の解析、相関係数の検定(Pearsonの積率相関係数)の順で選択します。

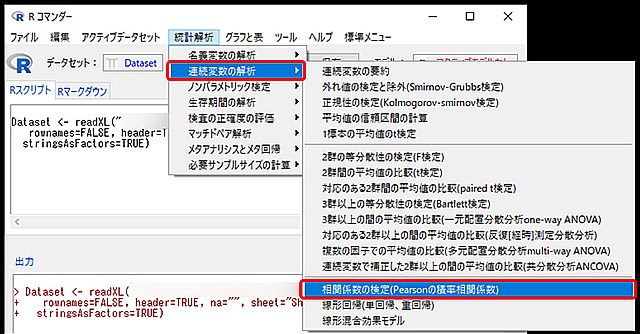
4.相関係数の検定(Pearsonの積率相関係数)のウィンドウが開きます

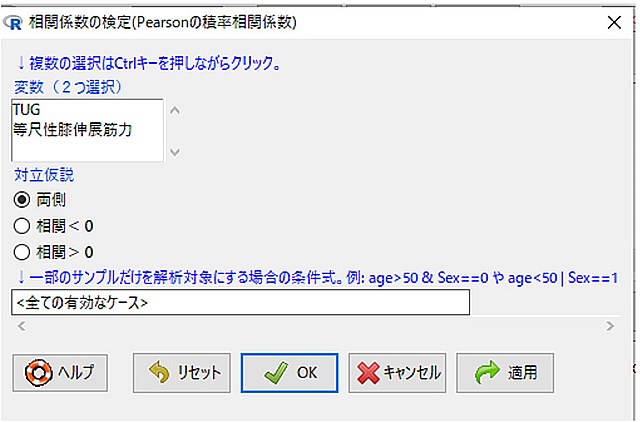
5.次に相関関係を求めたい変数をCtrlキーを押しながら選択します。

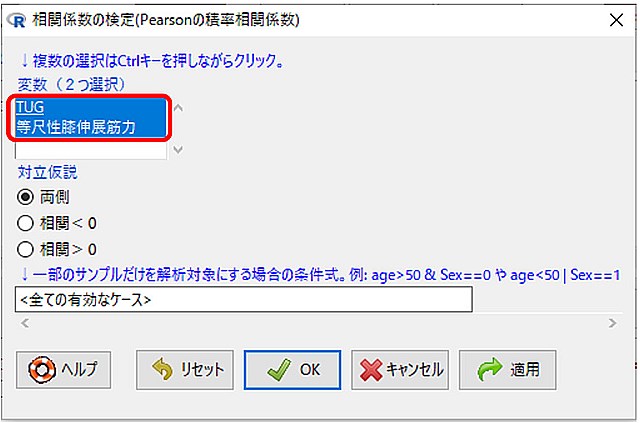
6.対立仮説のところは、両側にしておけば問題ないでしょう

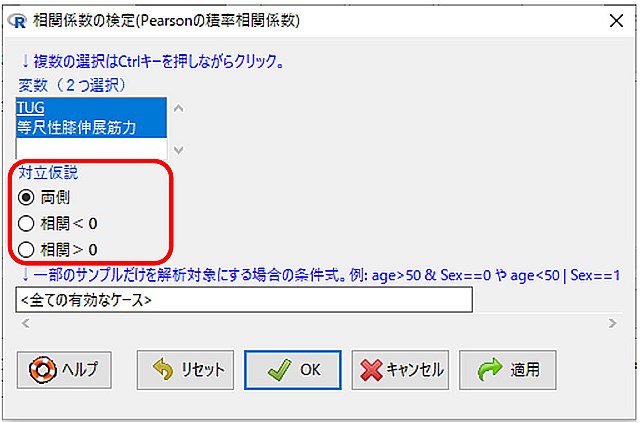
7.OKを押します

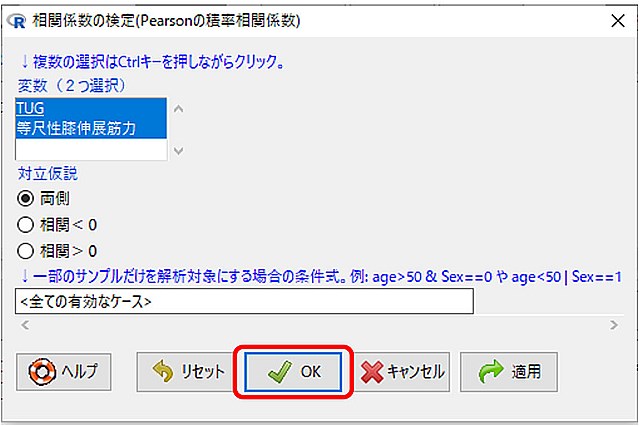
8.Pearsonの積率相関係数と検定が完了します。この時、図も作成されます。

目次に戻る

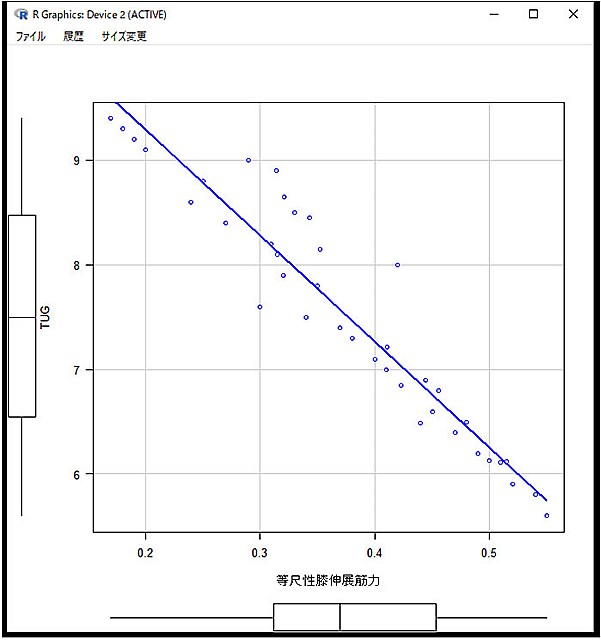
EZRの結果の見方

EZRの結果の見方がわかりにくい方もいると思うので、見方を説明します。

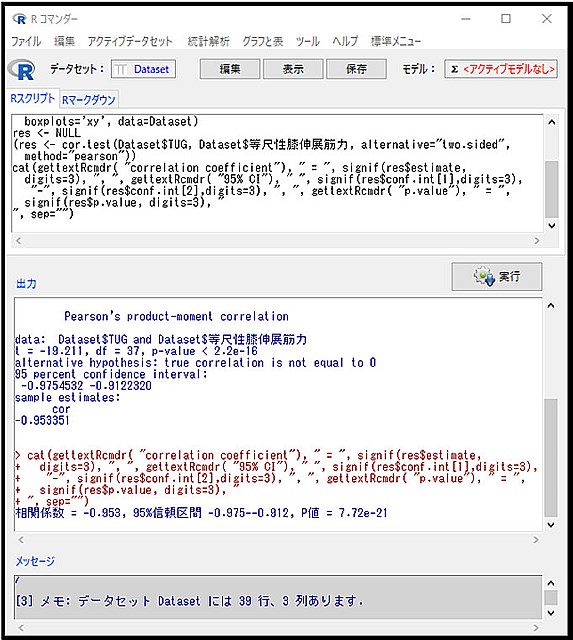
計算した結果は、このように出力のところに出ていると思います。

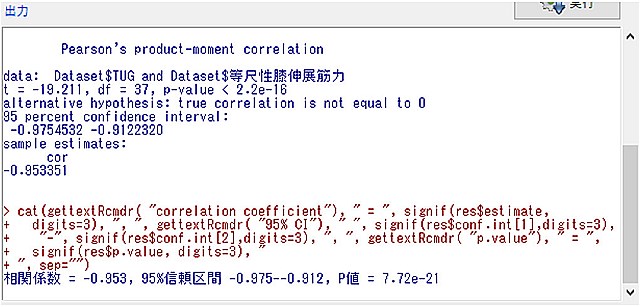
必要な情報は、下図の赤線の部分になります。ここを見ればよいです。

ピアソンの積率相関係数： -0.953
95%信頼区間： -0.975　-　-0.912
P値： 7.72e-21(＊e-21とは、10の－21乗の意味)

目次に戻る

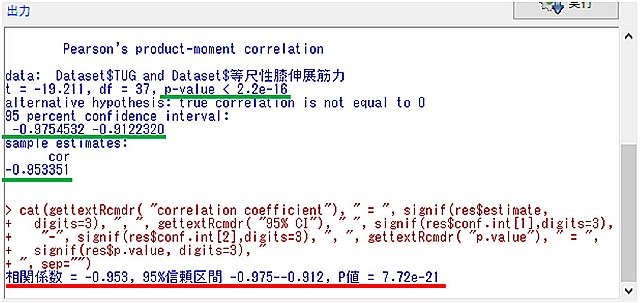
補足(結果の意味を日本語に翻訳)

結果は、こんな風に書いています。

Pearson’s product-moment correlation(ピアソンの積率相関)

data: Dataset$TUG and Dataset$等尺性膝伸展筋力
t = -19.211, df = 37, p-value < 2.2e-16
⇒検定統計量t = -19.211, 自由度 = 37, p値 < 2.2e-16(2.2×10^-16)

alternative hypothesis: true correlation is not equal to0
⇒対立仮説：相関係数は0ではない

95 percent confidence interval:
-0.9754532 -0.9122320
⇒95%信頼区間は、 -0.9754532 -0.9122320

sample estimates:
cor
-0.953351
⇒相関係数-0.953351

> cat(gettextRcmdr( “correlation coefficient”), ” = “, signif(res$estimate,
+ digits=3), “, “, gettextRcmdr( “95% CI”), ” “, signif(res$conf.int[1],digits=3),
+ “-“, signif(res$conf.int[2],digits=3), “, “, gettextRcmdr( “p.value”), ” = “,
+ signif(res$p.value, digits=3), ”
+ “, sep=””)
相関係数 = -0.953, 95%信頼区間 -0.975–0.912, P値 = 7.72e-21

目次に戻る